由生产实践的经验可知，顺序移动生产方式会导致大量设备闲置。因此，如果一定数量的某种工件成批生产，就需要考虑将这批工件分批，分批结果产生的批次数量、每批次包含的工件数量都会影响到设备利用率和生产管理方式。批次越多(即每批包含的工件数量越少)，则转运时间增加，同时生产管理更为复杂。批次越少，则设备闲置时间越长。如何合理安排工件数量和批次数量，就是所谓的分批调度问题。

1 车间分批调度问题

    目前，对车间级分批问题的研究主要集中在流水车间。流水车间中把工件分成几个子批加工而不是整批一起加工，其好处是显而易见的。首先，各个子批加工完某道工序后，不必等待所有同类工件都加工完这道工序就可以立即进行下道工序的加工，从而缩短了Cmax；其次，同时加工的工件很多，降低了对库存的要求，节省了成本；第3，工件拖期的可能性也降低了。对流水车间的分批调度问题的研究较为成熟，其应用也较为广泛。

    对于作业车间中的分批漏度问题，尽管较为复杂，但也取得了一些有用的成果。Low等对分批调度问题进行了比较深入的研究，建立了分批调度问题的数学模型，并利用仿真方法进行了实验，得出的结论认为将工件分批时将其等分更有利于缩短Cmax。。等分批是常用的分批策略，很多分批方法都优先采用等分批的策略，当使用等分批已经不能使结果更加优化时，才考虑用其它分批策略。例如Jeong等提出了4种分批策略；FBS、EBS、MBS、RBS，其中EBS就是等分批策略。Wanger和Ragatz采用仿真的方法来研究作业车间的调度问题也得到了类似的结论：分批可以缩短Cmax，同时也可以降低工件拖期的可能性。黄刚等对作业车问分批调度进行了研究，提出了一种基于非等分批策略的遗传退火两阶段算法。

2 作业车间分批调度问题的数学模型

    分批问题基于如下假设：设作业车间里有M台机器，某段时间有N类工件需要加工，每类工件都有一定的数量。假设每个工件在任一台机器上的加工工序都有且只有一个。每台机器任一时刻只能加工一个工件，任一工件同一时刻只能被一台机器加工。不同种类工件接连加工时需要工序准备时间，同类工件连续加工时不需要工序准备时间(第一个工件除外)。

    显然，工序准备时间是一个与工序有关的常量，与每批工件包含的工件个数无关。问题的目标是将各类工件划分为合理的加工批次，使得Cmax。最小，或者综合制造成本最小，或者两者的加权值最小。

    为了描述方便，首先给出模型中要用到的符号。

    3.1 算法一：从机器负荷角度出发的分批算法

    该算法来源于文献对FMS系统工件分批调度设计的算法的分批预处理部分。算法的基本思想是：当不同类工件的总加工时间相差很大时，若不分批(仍按整批加工)，则加工时间长的工件会长时间占有机床，从而使其它种类的工件处于等待状态而不能被及时加工，同时有些机床会由于得不到工件而处于空闲状态。因此，将加工时间很长的工件适当划分子批，既可以减少工件的等待时间，又可以减少机床的空闲时间，从而缩短Cmax。

    该算法先计算各类工件的整批加工时间之和。然后求出加工时间平均值，再将各类工件的整批加工时问与平均加工时间作比较，确定是否要划分子批以及批数是多少。

    算法的具体流程如下。

    步骤1：计算每类工件的整批加工时间TTi。(i=1，2，…，n)。

    步骤2：计算总加工时间TT，将总加工时间除以工件数，求出平均加工时间TT。

    步骤3：计算每类工件应划分的子批数，Bi=int(TT)/TT+1，作为工件应划分的子批数。

    从该算法的原理和流程来看，使用政算法所能产生的总批数不会很多，被分批的是那些加工时间特别长的工件类。  3.2 算法二：从最大完成时间出发的分批算法

    算法的基本思想是：当车间只加工一类工件时，必定存在一个最优的分批方案。先确定每一类工件单独成批加工时应该划分的子批数，然后基于这种分批，采用确定性调度算法求出较好的蒯度方案。显然，这种算法是一种两层优化算法。在求分批数时，把工序准备时间也加进加工时间内，而不遵循同类工件连续加工时不需准备时间的规定，一方面是考虑到遗传算法生成的调度方案有很大可能是同类工件的不同子批不连续加工；另一方面也是为了限制批数。

    计算每类工件单独加工时的Cmax，可以这样做：首先确定分批数；然后计算每个子批包含的工件数，计算每道工序的加工时间，并加上工序准备时间。这时每个子批可看成一个独立的工件，所有工件在车间中的加工方式便成了平行移动方式，按式(9)计算一类工件单独加工的最大完成时间：

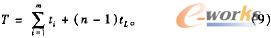
    其中，T为最大完成时间；m为工序数；n为批数；ti为第i工序的加工时间；tL为最长工序的加工时间。算出某种批数情况下的最大完成时间，与前一种批数的最大完成时间比较，若前者大，则算法停止，否则继续增加分批数。

    该算法的流程如下。

    步骤1：初始化参数，令i=1，loti=1。

    步骤2：将工件i分成lot。批，计算每批每道工序的加工时间，再加上每道工序前的工序准备时间。

    步骤3：按公式(13)计算最大完成时间。

    步骤4：若loti=1，loti++。否则比较分成loti批时的最大完成时间与分成(loti-1)批的最大完成时间，如果前者大，转步骤5，否则转步骤2。

    步骤5：存储并输出loti。

    步骤6：i++，如果i小于工件种类数，返回步骤2。否则结束算法，输出loti其中i=l，2，…，n。

    3.3 算法三：遗传退火两阶段算法

    该算法与上面2种算法的区别在于本算法用遗传算法产生初始分批方案，再用模拟退火算法求解调度方案。这可以看成一个两层的算法结构，上层为产生分批方案的遗传算法，下层为产生调度方案的模拟退火算法。下层模拟退火算法相当于上层遗传算法的一个解码函数，被上层频繁调用。

    算法流程大致如下。

    步骤1：初始化各参数，包括种群个体数、遗传数等等；

    步骤2：产生初始种群；

    步骤3：对种群代表的分批方案分别编码，传递给下层模拟退火算法解码；

    步骤4：计算种群各染色体的适配值，按概率用轮转法选出个体进行交叉操作；

    步骤5：进行变异操作；

    步骤6：判断是否满足算法结束条件，若满足，结束算法，否则转步骤3。

    各层中遗传算法和模拟退火箅法的详细描述见文献。

4 作业车间分批调度算法的对比分析

    实验样本取文献中的6×6的生产环境(6工件，6机器)，基础数据如下。式(10)～式(12)中行数为工件数．列数为工序数。
 

    4.1不同类工件总加工时间的差异程度对分批的影响

    实验I

    实验I主要考察当不同种类工件之间加工时间差异较小时各算法的计算效果。各类工件要加工的数量见表1。

    表1  实验I已知数据

    用各工件单独加工时的总加工时间与平均加工时间之比来衡量工件加工时间的差异程度。由于无法预料会有多少次工序准备工作，所以工序准备时间不包括在总加工时间中。从表1中的数据和工序准备时间阵可以看出，各工件总加工时间相差不大，且工序准备时间较短。计算结果见表2。

表2  实验I结果及标准差

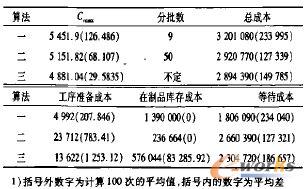
    从表2中的数据可看出，当不同种类工件之间加工时间差异不大时，算法一的Cmax结果较差，算法二相对较好一些，但分批数较多。算法一在这种情况下得不到较好的结果是由于它采用将工件各自的加工时间与平均加工时间相比较，然后确定分批数，在各类工件加工时间差异不大的情况下会导致分批数过小，从而搜索不到比较优化的结果。算法三是这3种算法中效果最好的，这一方面因为它没有使用等分批的原则，使解的存在范围扩大了不少；另一方面可能是因为分批阶段和调度阶段不再是2个完全独立的阶段，调度的结果对分批方案存在反馈作用。从这个实验的结果中也再次证明：在作业车间调度中，分批确实能够缩短Cmax。即使附加了一个工序准备时间矩阵，分批后的Cmax仍比不分批的Cmax要小。例如，不分批的情况下最好的Cmax为5500，而分批后平均仅为4881.04，比不分批的最好值缩短了11.25％以上。 实验Ⅱ

    实验Ⅱ主要考察不同工件加工时间差异较大的情况。各类工件要加工的数量见表3。

表3  实验Ⅱ已知数据

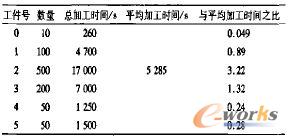
    表3中这里各工件的总加工时间差异较大，加工时间最短的工件只占平均时间的5％。而加工时间最长的工件是平均加工时间的3倍以上。各算法的计算结果见表4。

表4  实验Ⅱ结果及其标准差

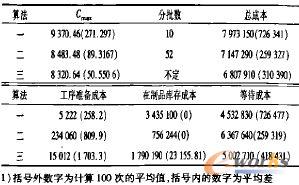
    从表4可看出，计算结果中仍是算法三最好，算法二次之，算法一最差。

    实验I和Ⅱ各工件分批数见表5。

表5  分批数的比较

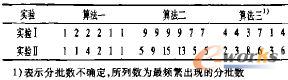
    对于不同工件加工时问差异较大的情况，算法一生成的分批数仍较少，加工时间相对较短的工件0、1、4、5没有被拆分，而加工时间相对最长的两个工件2和3被拆分了，算法一的Cmax优化结果平均为9370.46，与不分批的情况下的最大完成时间17609相比，有了大幅的提高。同样算法二的分批数非常多，且加工时间越长，被拆分的子批数就越多，其比算法一又有所提高。算法三的分批数界于前两者之闻，其优化结祟仍是3种算法中最好的。

    4.2 工序准备时间的长短对分批的影响

    实验Ⅲ

    工序准备时间较长时，分批越多会使工序准备时间越多，则Cmax也越大。实验Ⅲ考虑工序准备时间较长的情况。保持实验I其他参数不变，将工序准备时间数据改为：

    由于工序准备时间较长，因此如果分批数过多，就会有很多时间花在工序准备工作上，从而抵消由分批带来的Cmax缩短效应。实验结果如表6。

表6  实验Ⅲ结果及其标准差
 

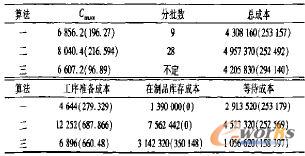
    由表6中数据可知，在实验Ⅲ的情况下，算法一有了用武之地，其计算结果不论从时间上还是从成本上看，都是比较理想的。算法二由于产生的批数过多，需要做很多工序准备工作，浪费了很多时问和金钱，产生的结果很差。算法三由于其独特的方法，产生的结果仍旧是三者之中最好的。顺便说明。如果不分批，Cmax为6600，总成本为4293600。而算法一的最好结果Cmax和总成本分别为6510，4145700，仅有小幅提高；算法三的最好结果分别是6480，4417600，成本竟有所上升。这是因为算法都是以缩短Cmax为优化目标，优化过程中没有考虑成本的缘故。

5 结果分析

    从以上模拟计算可以看到：

    1)差异程度越大，分批后效果越明显，可分批数越多。差异程度不大的情况，也可引入分批，一方面利用分批产生的交叠作用进一步缩短加工时间；另一方威增加了在制品数量，节省成本。

    2)工序准备时间越长，分批数越少。工序准备时间的长短是相对长度，以单独整批加工时总工序准备时间与总加工时间之比来衡量。

    3)工序数不多，单位工序准备成本不大的情况下，可忽略工序准备成本，只考虑在制品序存成本和等待成本。反之不能忽略。比较好的分批数与3种成本都有关系，一般来说，最优分批数与单位工序准备成本和单位等待成本成反比，与单位在制品库存成本成正比。由于它们之间的关系很复杂，以成本为优化目标，采用邻域搜索算法来寻找比较好的解是一个很好的方法。

    4)工件种数和工序数这两个因素的影响通过其它因素表现出来。例如工序数的增加使工穿准备成本以及等待时间增加等。它们的影响机理本文没有深入探讨，还需要进一步研究。综合实验结果，给出各算法的评价如表7

表7  算法评价

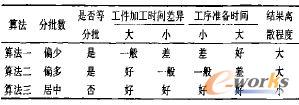
6 结束语

    对解决作业车间分批调度问题的几个算法进行了计算对比分析，通过实验数据总结了影响分批的几个因素。这些因素包括工件加工时间的差异程度、工序准备时问的长短、成本、工件数和工序数等。计算结果表明，遗传退火两阶段算法优化效果较好。算法的适应性较强。但是，由于搜索空间的增大，导致计算时间较长。一个6×6问题通常需要200s左右(20代20个体，初温20000，降温系数0.95)。尽管如此，遗传退火两阶段算法的方法仍然可以为今后的算法设计提供参考。