线性回归

线性回归是一种找到最适合一组点的直线或超平面的方法。本模块会先直观介绍线性回归，为介绍线性回归的机器学习方法奠定基础。

人们早就知晓，相比凉爽的天气，蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来，专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录。Ruth 阿姨将她喜爱的蟋蟀数据库作为生日礼物送给您，并邀请您自己利用该数据库训练一个模型，从而预测鸣叫声与温度的关系。

首先建议您将数据绘制成图表，了解下数据的分布情况：

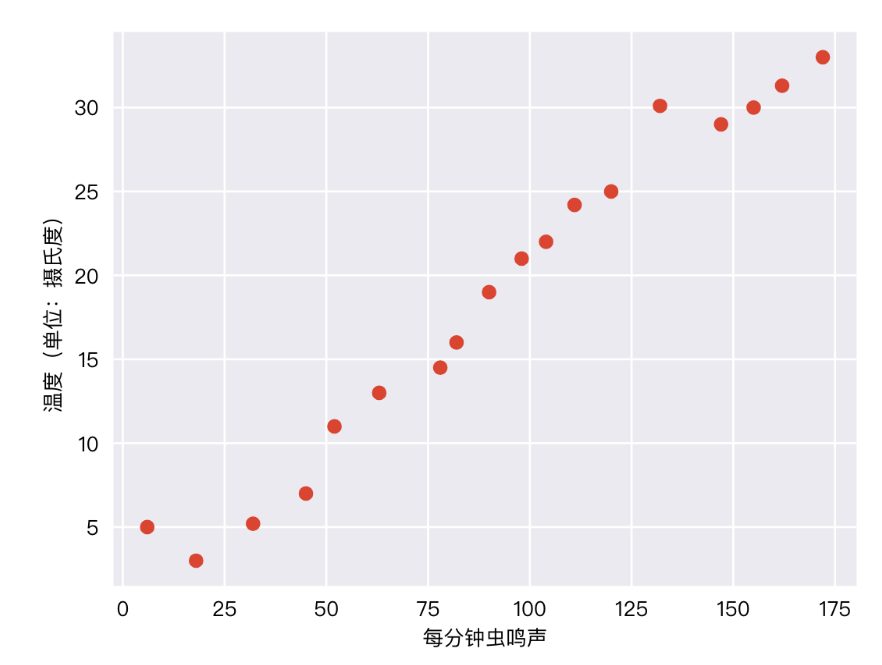
图 1. 每分钟的鸣叫声与温度（摄氏度）的关系。

毫无疑问，此曲线图表明温度随着鸣叫声次数的增加而上升。鸣叫声与温度之间的关系是线性关系吗？是的，您可以绘制一条直线来近似地表示这种关系，如下所示：

图 2. 线性关系。

事实上，虽然该直线并未精确无误地经过每个点，但针对我们拥有的数据，清楚地显示了鸣叫声与温度之间的关系。只需运用一点代数知识，您就可以将这种关系写下来，如下所示：

y=mx+b

其中：

• y 指的是温度（以摄氏度表示），即我们试图预测的值。

• m 指的是直线的斜率。

• x 指的是每分钟的鸣叫声次数，即输入特征的值。

• b 指的是 y 轴截距。

按照机器学习的惯例，您需要写一个存在细微差别的模型方程式：

y′=b+w1x1

其中：

• y′ 指的是预测标签（理想输出值）。

• b 指的是偏差（y 轴截距）。而在一些机器学习文档中，它称为 w0。

• w1 指的是特征 1 的权重。权重与上文中用 m 表示的“斜率”的概念相同。

• x1 指的是特征（已知输入项）。

要根据新的每分钟的鸣叫声值 x1 推断（预测）温度 y′，只需将 x1 值代入此模型即可。

下标（例如 w1 和 x1）预示着可以用多个特征来表示更复杂的模型。例如，具有三个特征的模型可以采用以下方程式：

y′=b+w1x1+w2x2+w3x3

关键字词

训练与损失

简单来说，训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值。在监督式学习中，机器学习算法通过以下方式构建模型：检查多个样本并尝试找出可最大限度地减少损失的模型；这一过程称为经验风险最小化。

损失是对糟糕预测的惩罚。也就是说，损失是一个数值，表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确，则损失为零，否则损失会较大。训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。例如，图 3 左侧显示的是损失较大的模型，右侧显示的是损失较小的模型。关于此图，请注意以下几点：

• 红色箭头表示损失。

• 蓝线表示预测。

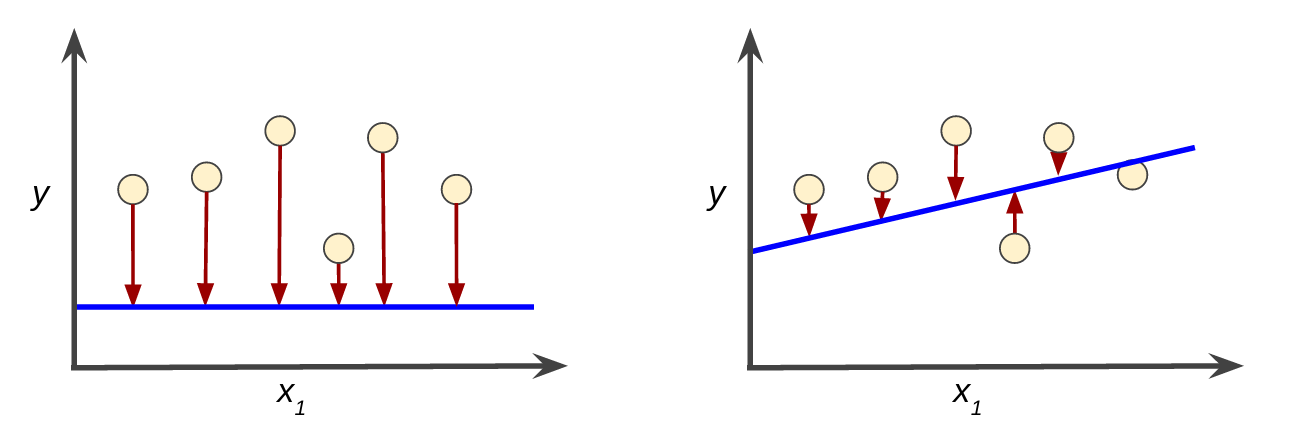
图 3. 左侧模型的损失较大；右侧模型的损失较小。

请注意，左侧曲线图中的红色箭头比右侧曲线图中的对应红色箭头长得多。显然，相较于左侧曲线图中的蓝线，右侧曲线图中的蓝线代表的是预测效果更好的模型。

您可能想知道自己能否创建一个数学函数（损失函数），以有意义的方式汇总各个损失。

平方损失：一种常见的损失函数

接下来我们要看的线性回归模型使用的是一种称为平方损失（又称为 L2 损失）的损失函数。单个样本的平方损失如下：

  = the square of the difference between the label and the prediction
  = (observation - prediction(x))2
  = (y - y')2

均方误差 (MSE) 指的是每个样本的平均平方损失。要计算 MSE，请求出各个样本的所有平方损失之和，然后除以样本数量：

MSE=1N∑(x,y)∈D(y?prediction(x))2

其中：

(x,y)

指的是样本，其中

• x 指的是模型进行预测时使用的特征集（例如，温度、年龄和交配成功率）。

• y 指的是样本的标签（例如，每分钟的鸣叫次数）。

• prediction(x) 指的是权重和偏差与特征集 x 结合的函数。

• D 指的是包含多个有标签样本（即 (x,y)）的数据集。

• N 指的是 D 中的样本数量。

虽然 MSE 常用于机器学习，但它既不是唯一实用的损失函数，也不是适用于所有情形的最佳损失函数。